Interferența nelocalizată - Dispozitivul Young
Pentru realizarea interferenței luminii prima problemă importantă este cea a realizării a două surse coerente.
O soluție practică a acestei probleme a găsit-o în 1802 Thomas Young (1772-1829). Schița de principiu a dispozitivului utilizat de Young pentru realizarea interferenței luminii este prezentată în figura 1. Sursa de lumină, S, este un filament incandescent în fața căruia se află un flltru; acesta lasă să treacă numai radiațiile care au o anumită lungime de undă, fie ea λ0 în vid (și în aer). Lumina monocromatică ajunge la un ecran prevăzut cu două fante dreptunghiulare situate foarte aproape una de alta. Distanța de la sursă la ecran este de ordinul zecilor de centimetri. Fantele sunt foarte înguste (0,1 - 0,2 mm), iar distanța dintre ele este mai mică de 1 mm.
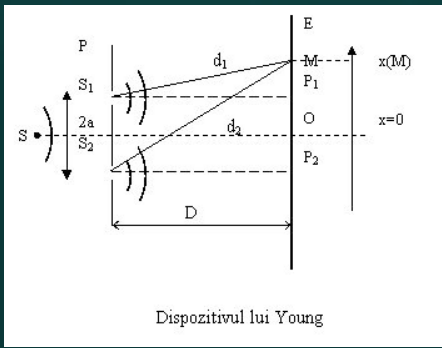
Conform principiului lui Huygens cele două fante devin surse secundare de la care pleacă două unde spre un al doilea ecran situat la câțiva metri de primul ecran și paralel cu acesta. Aceste două unde provin de la aceeași sursă, deci sunt corerente. Chiar dacă are loc o variație a fazei inițiale a luminii emise, diferența de fază dintre undele emise de sursele secundare se păstrează aceeași. Pe al doilea ecran se formează franje de interferență în forma unor benzi paralele luminoase și întunecate, dispuse alternativ.
Schița experimentului lui Young este prezentată în figura 2:
Fig. 2.
unde: S - sursă de lumină (filament incandescent în fața căruia se așază un flitru optic cu lumină monocromatică);
F1, F2 - fante (deschideri foarte înguste într-un paravan opac);
d - distanța dintre sursă și paravanul opac;
D - distanța dintre paravan și ecran;
2l - distanța dintre fante;
P - un punct oarecare de pe ecran situat la distanțele r1 și r2 față de F1 și F2.
Din figura 2 rezultă:
r12 = (x - l)2 + D2
r22 = (x + l)2 + D2 (1)
deci
(r2 - r1)· (r1+r2) = 4 · x · l (2)
Cum distanțele x și l sunt de ordinul fracțiunilor de milimetru, iar distanța D de ordinul mai multor sute de milimetri, se poate considera că r1 + r2 ≈ 2D. Rezultă coordonata punctului de pe ecran în care se vede franja de interferență:
x = (r2 - r1) · D / 2l = δ · D / 2l (3)
unde δ = diferența de drum optic dintre radiații.
Condiția ca în P să existe un maxim de interferență este ca diferența de drum optic să fie un multiplu întreg al lungimii de undă (δ = k · λ ). Rezultă poziția franjei luminoase de ordin k (distanța de la ea la punctul central O):
xk = k · λ · D / 2l, k = 0, 1, 2, 3, .... (4)
Pentru k = 0 se obține x0 = 0. Această franjă luminoasă al cărui centru este în punctul C se numește franjă centrală.
Confom relației precedente, distanța dintre două franje vecine, numită interfranjă, este dată de relația:
i = xk+1 - xk = λ · D / 2l
i = λ D / 2l (5)
Din această relație se vede că interfranja nu depinde de k, deci franjele luminoase vecine sunt echidistante. Regiunea din spațiu în care se prind franjele de interferență fiind foarte mare, se spune că interferența este nelocalizată.
Relația precedentă permite determinarea lungimii de undă. Se măsoară interfranja i și, cunoscându-se distanța 2l dintre fantele paravanului și distanța D dintre paravan și ecran se poate calcula lungimea de undă cu relația:
λ = 2l · i / D (6)
Dacă se efectuează experiența lui Young cu lumină albă pe ecran se obține o franjă centrală albă însoțită de ambele părți de franje colorate începând cu violet și terminând cu roșu (spectrul luminii albe incidente). Acest rezultat se explică dacă se observă că radiațiile cu lungimi de undă diferite nu interferă între ele: pentru un ordin k dat, xk depinde de lungimea de undă. Aceasta înseamnă că pozițiile franjelor luminoase de ordin k vor fi ușor diferite în funcție de λ. Fiecare radiație monocromatică determină apariția unui sistem propriu de franje, interfranjele depinzând de lungimea de undă. Deoarece franjele centrale au toate aceeași poziție, în zona respectivă se suprapun toate franjele care recompun lumina albă.
https://youtu.be/61KlIK3grIw



Comentarii
Trimiteți un comentariu